This my ideas to avoid the more frustration while mapping for dæmon based games. Dæmon is an open source engine, so Unvanquished is not only a game, it's also fun stuff to hack with. So, we must offer a nice mapping experience to see people having fun to hack with the dæmon engine and Unvanquished.
You know, netradiant and q3map2 are very old, they do not compete with newer solutions, but it's not a problem for many enthusiasts if it works for them? Even if it's dated, it's not a problem for many enthusiasts if they can do something they can be proud of, if they can do it without frustration. The main problem is not having plenty of shiny functionalities, the main problem is when basic functionalities are hard to deal with.
1. Source versioning
Netradiant renumbers all changes entities and patches every time it saves the map, so every minor change leads to thousands of line changes. My map cutter can denumber the map files and I'm using it every time before commit. A very good thing would be to have an option in netradiant to not number the entities by default. It's good to keep a way to number entities to be able to debug the file by hand (mapping the vim way) while reading a compilation log.
By the way, my map cutter knows how to renumber a map. Due to legacy stuff, netradiant must keep the do not number the entities option deactivated by default (opt-out). By the way, it could be a per-game default setting (we can imagine that mappers for dæmon based game get a nice profile without needing to tweak it, while mappers for legacy games keep the legacy behavior, since they will already miss all the other enhancements).
To help managing source cleanly, the build process must be manageable by a dedicated build tool, and the build tool must allow out of tree compilation.
1. Build process
My pak mallet can handle the build of a complete pak including asset compression and map compilation, based on a per-file rule list it can auto update itself. I have many improvements to do but the basis are there.
2. Source based compilation
The mapper must be able to keep a clean source tree and must be able to compile and test his production against a clean environment. It means both dæmon, netradiant and q3map2 must be able to load any paks from any directory the mapper wants (pak dependency…), they must be able to load pk3dir, and q3map2 must be able to compile from a source dir to a build dir. The mapper must be able to never load his built map from the source dir (that way he is only testing final assets).
Dæmon already allows all of that. I have patches pending for q3map2 that allows arbitrary pakpath loading and out of tree compilation. It looks like netradiant knows how to load pk3dir (there was a something done) but it seems q3map2 still lacks this support.
Netradiant and q3map2 must have an option to not load user game data in pkg dir to not mess with foreign stuff.
Also, q3map2 must have an option to not rely on shaderlists and load all shaders since there will be explicit options to get a clean source tree.
3. Usability
The mapper must be able to load a map in netradiant from command line or using file association.
4. Fast and easy testing
This is now the major part, and all these ideas are doable. There is two axis: doing things fast, and integrating tools.
gimhael added a fallback lightgrid in dæmon (skipping lightgrid compilation saves a lot of time) and I have some pending changes to speed up the lightmap allocation process in q3map2.
Dæmon allows to send command to an existing instance and to set the camera in an arbitrary position (it still lacks the ability to set the angle in all directions), so, it could be possible to netradiant having the engine loaded in another window and having the camera in the engine following the netradiant camera.
Dæmon must be able to load a map without intermission and spawn entities, spawning floating in the middle of the map, and Dæmon must be able to load a layout from a pk3[dir] (I read somewhere that tremulous was able to use alternate layout in pk3, is it still true for Dæmon and is the default layout can be an external file in the pk3?), so the mapper will not have to put the structures entities in the map but can layout his map in game directly. It also allows to modify the default layout without having to alter the bsp.
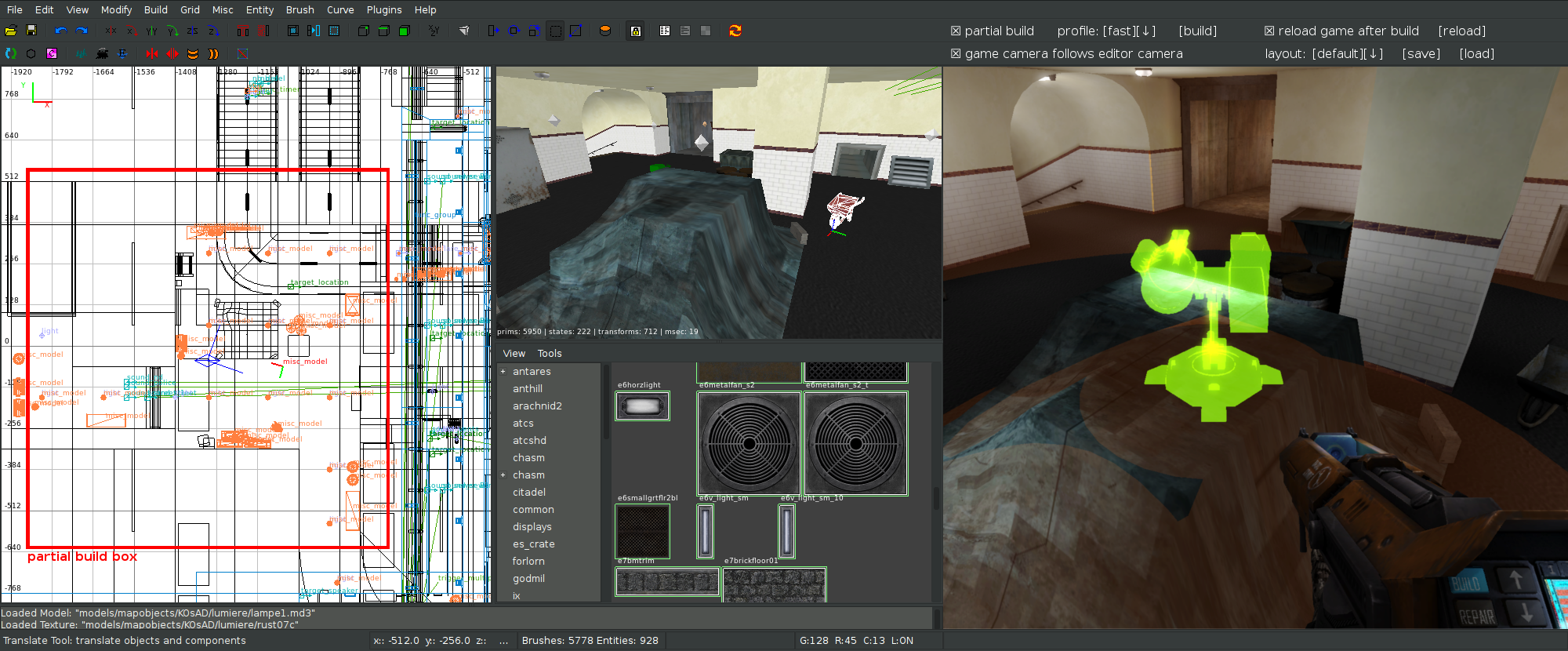
Netradiant must allow to define a box with the camera in center of the box (the volume of the box must be modifiable by the user). This box coordinates and size must be exportable by netradiant (in a temporary file for example), so q3map2 can read it. q3map2 must be able to cut out everything which is outside of this box and build valid edges with a visible recognizable texture on box edges to prevent leaking. This functionality will allow the mapper to render only a part of the map. It's very important to save hours when the mapper tests his lightmaps.
For example, this whole room takes only 43s to render with 5 radiosity bounces (but I spent hours to manually cut out everything outside):
This very big room room takes only 43s to render, But the whole map takes about 43min to render… So, with that option the mapper will be able to test his rendering in less than minutes! The mapper will be able to test his rendering room per room!
There was also some work done on dæmon's side to allow engine embedding. It can allow the engine to be embedded in a netradiant Window.
Imagine : the mapper have the mapping editor window, the basic 3D renderer of netradiant to edit stuff, and the engine window. Clicking one button will compile the current room, send the devmap, noclip and setviewpos commands to the engine so the engine reload the map in the current room. The mapper can see the rendering in game, layout his map (and save the ingame layout from a netradiant button) etc. If the mapper ticks a checkbox, the compilation only compiles the current room (everything inside the box that follow his camera) and reloads the current room in game in less than a minute!
I'm thinking about something like that: